16. Implement Naive Bayes C++
Implementing Naive Bayes
In this exercise you will implement a Gaussian Naive Bayes classifier to predict the behavior of vehicles on a highway. In the image below you can see the behaviors you'll be looking for on a 3 lane highway (with lanes of 4 meter width). The dots represent the d (y axis) and s (x axis) coordinates of vehicles as they either…
- change lanes left (shown in blue)
- keep lane (shown in black)
- or change lanes right (shown in red)
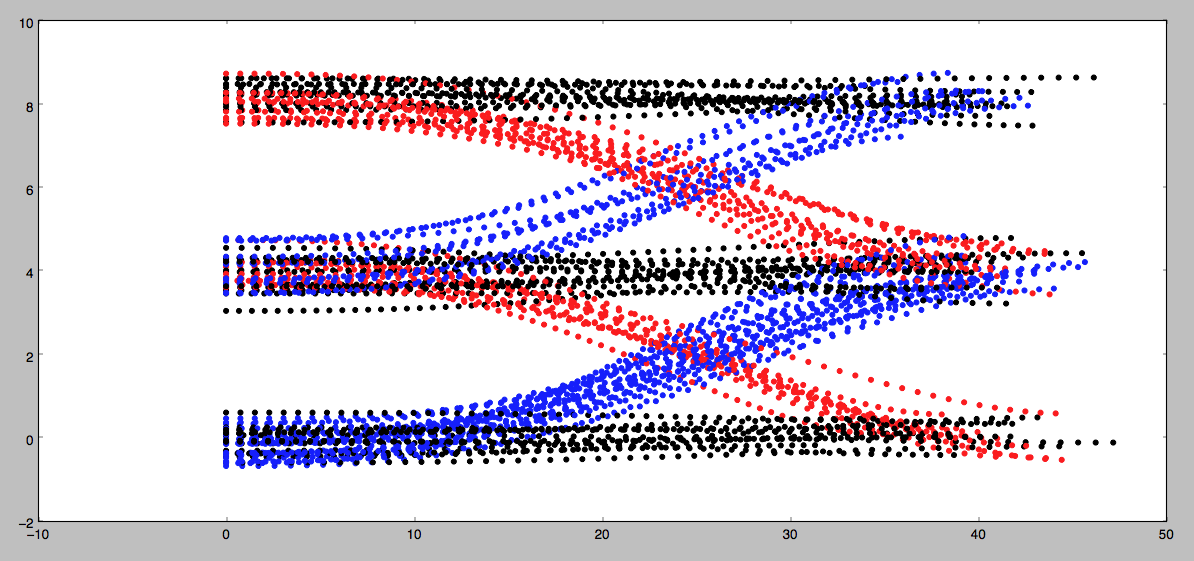
Your job is to write a classifier that can predict which of these three maneuvers a vehicle is engaged in given a single coordinate (sampled from the trajectories shown below).
Each coordinate contains 4 features:
- s
- d
- \dot{s}
- \dot{d}
You also know the lane width is 4 meters (this might be helpful in engineering additional features for your algorithm).
Instructions
-
Implement the
train(data, labels)method in the classGNBinclassifier.cpp.Training a Gaussian Naive Bayes classifier consists of computing and storing the mean and standard deviation from the data for each label/feature pair. For example, given the label "change lanes left” and the feature \dot{s} , it would be necessary to compute and store the mean and standard deviation of \dot{s} over all data points with the "change lanes left” label.
Additionally, it will be convenient in this step to compute and store the prior probability p(C_k) for each label C_k . This can be done by keeping track of the number of times each label appears in the training data.
-
Implement the
predict(observation)method inclassifier.cpp.Given a new data point, prediction requires two steps:
- Compute the conditional probabilities for each feature/label combination . For a feature x and label C with mean \mu and standard deviation \sigma (computed in training), the conditional probability can be computed using the formula here :
p(x = v | C) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp^{-\frac{(v-\mu)^2}{2\sigma^2}}Here v is the value of feature x in the new data point.
- Use the conditional probabilities in a Naive Bayes classifier. This can be done using the formula here :
y = \underset{k\in (1,\ldots, K)}{argmax } \,\,p(C_k) \prod^n_{i=1}p(x_i = v_i| C_k)In this formula, the argmax is taken over all possible labels C_k and the product is taken over all features x_i with values v_i .
-
When you want to test your classifier, run
Test Runand check out the results.
NOTE
: You are welcome to use some existing implementation of a Gaussian Naive Bayes classifier. But to get the
best
results you will still need to put some thought into what
features
you provide the algorithm when classifying. Though you will only be given the 4 coordinates listed above, you may find that by "engineering" features you may get better performance. For example: the raw value of the
d
coordinate may not be that useful. But
d % lane_width
might be helpful since it gives the
relative
position of a vehicle in it's lane regardless of which lane the vehicle is in.
Helpful Resources
Extra Practice
Provided in one of the links below is
python_extra_practice
, which is the same problem but written in Python that you can optionally go through for extra coding practice. The Python solution is available at the
python_solution
link. If you get stuck on the quiz see if you can convert the python solution to C++ and pass the classroom quiz with it. The last link
Nd013_Pred_Data
has all the training and testing data for this problem in case you want to run the problem offline.
Start Quiz:
INSTRUCTOR NOTE:
Students have reported Load_State function in main.cpp is not loading data properly from train_states.txt and test_states.txt since istringstream is not implemented for comma (',') separated data. Several students have found working solutions here , that may help in determining your own solution.