27. Implement Quintic Polynomial Solver C++
Implement a Quintic Polynomial Solver
In this exercise you will implement a quintic polynomial solver. This will let you take boundary conditions as input and generate a polynomial trajectory which matches those conditions with minimal jerk.
Inputs
Your solver will take three inputs.
-
start- [s_i, \dot{s_i}, \ddot{s_i}] -
end- [s_f, \dot{s_f}, \ddot{s_f}] -
T- the duration of maneuver in seconds.
Instructions
-
Implement the
JMT(start, end, T)function inmain.cpp -
Hit
Test Runand see if you're correct!
Tips
Remember, you are solving a system of equations: matrices will be helpful! The Eigen library used from Sensor Fusion is included.
The equations for position, velocity, and acceleration are given by:
and if you evaluate these at t=0 you find the first three coeffecients of your JMT are:
[\alpha_0, \alpha_1, \alpha_2] = [s_i, \dot{s_i}, \frac{1}{2}\ddot{s_i}]
and you can get the last three coefficients by evaluating these equations at t = T . When you carry out the math and write the problem in matrix form you get the following:
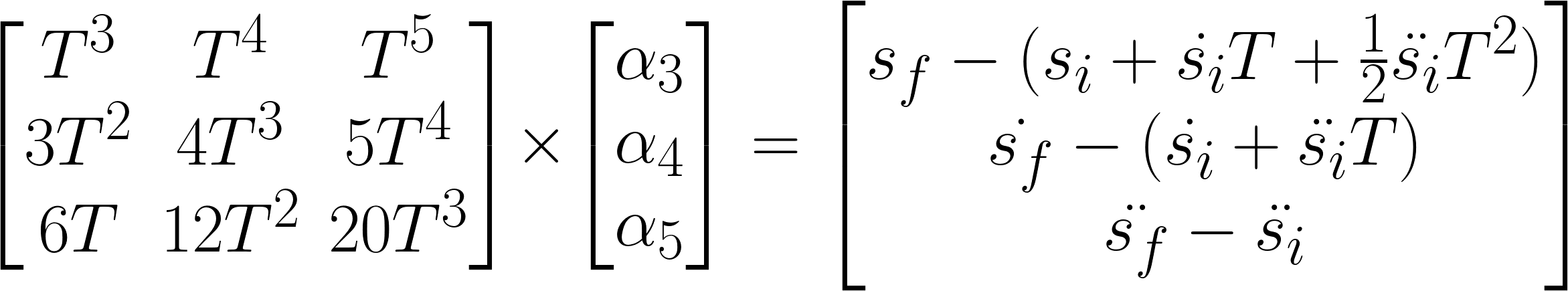
All these quantities are known except for \alpha_3, \alpha_4, \alpha_5
Start Quiz: